Prestižní ocenění výzkumu v oblasti spektrální teorie systémů řízení

Pracovníci ústavu přístrojové a řídicí techniky prof. Tomáš Vyhlídal a prof. Pavel Zítek získali prestižní ocenění za výsledek výzkumu v oblasti spektrální teorie systémů se zpožděním – jmenovitě za algoritmus QPmR pro výpočet kořenů charakteristických kvazipolynomů systémů se zpožděním [1].

Jedná se o ocenění výsledku třídou A pilíře II, metodiky hodnocení výsledků výzkumných organizací RVVI – 2014 (hodnocené období 2009-2013). Do pilíře II byl výsledek nominován spolu s dalšími významnými výsledky dosaženými na fakultách a ústavech ČVUT v Praze. Na základě odborného posouzení expertními panely, bylo z celé ČR vybráno 277 výsledků, které tvoří 20% nejlepších výsledků ze všech nominovaných.

Z ČVUT bylo třídou A oceněno celkem 14 výsledků. Počtem oceněných výsledků se ČVUT umístilo na třetím místě, a to za Akademií věd ČR a Univerzitou Karlovou v Praze.     

Algoritmus QPmR [1],[2], umožňuje výpočet rozsáhlých částí spekter kořenů kvazipolynomů, která jsou z funkcionální podstaty systémů se zpožděním nekonečná. Algoritmus lze použít jak k ověření stability, tak i k syntéze řízení této třídy systémů. V současné době výzkumný tým algoritmus využívá například při návrhu systémů tlumení vibrací s využitím algoritmů se zpožděním [3], [4], [5].

Příklad distribuce kořenů kvazipolynomu s „jednoduchou“ strukturou

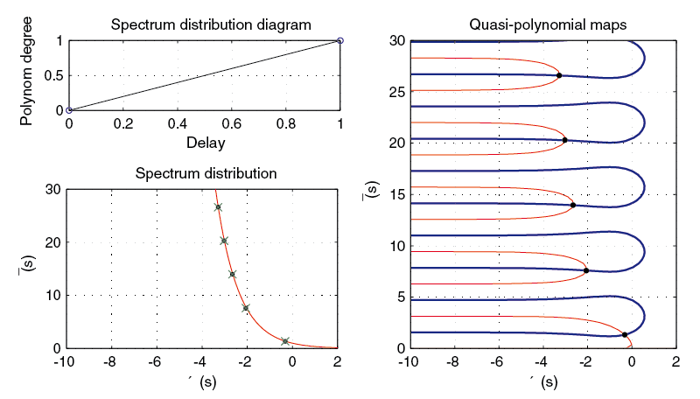Spektrum kvazipolynomu (Example 1 [2])
h(s) = s + exp(-s)

Algoritmus QPmR je založen na mapování charakterictického kvazipolynomu v komplexní rovině. Asymptotické vlastnosti spekter jsou získány s využitím distribučního diagramu.

Příklad distribuce kořenů kvazipolynomu se „složitější“ strukturou

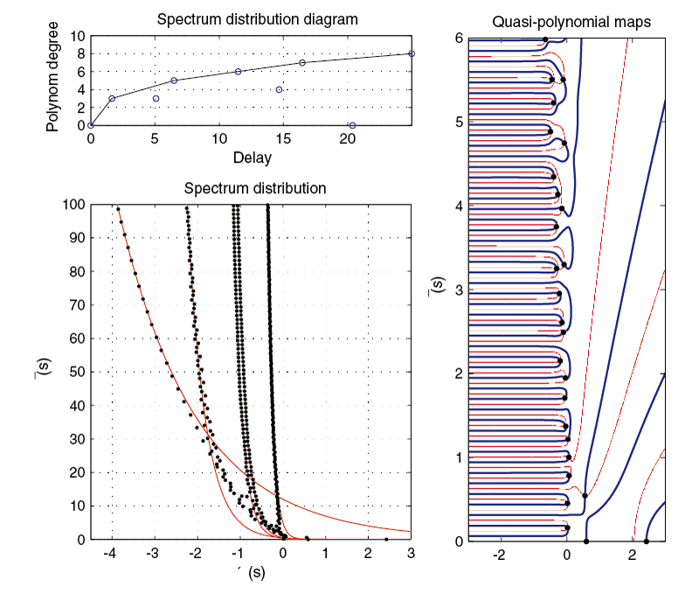Spektrum kvazipolynomu (Example 2 [2])

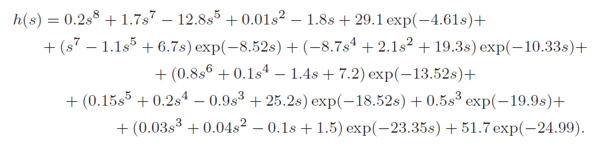Určení asymptotických vlastností nekonečných spekter kořenů kvazipolynomů pomocí QPmR algoritmu umožňuje hlubší analýzu stability a dominantních vlastností systémů se zpožděním.

Příklad distribuce kořenů kvazipolynomu neutrálního typu

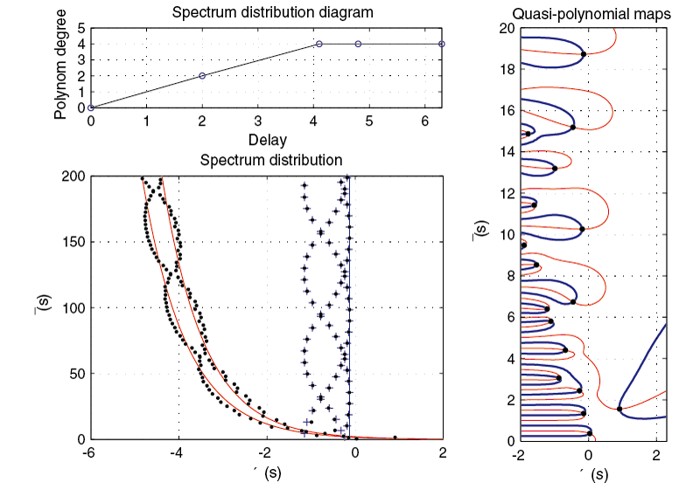Spektrum kvazipolynomu (Example 3 [2])

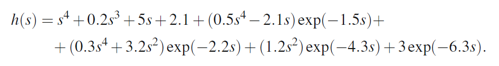Pro tzv. neutrální systémy je spektrální analýza složitější, vyžaduje vyšetření vlastností přidruženého exponenciálního polynomu, který je v tomto případě

Aplikace QPmR algoritmu v analýze spektrálních vlastností tvarovačů signálu

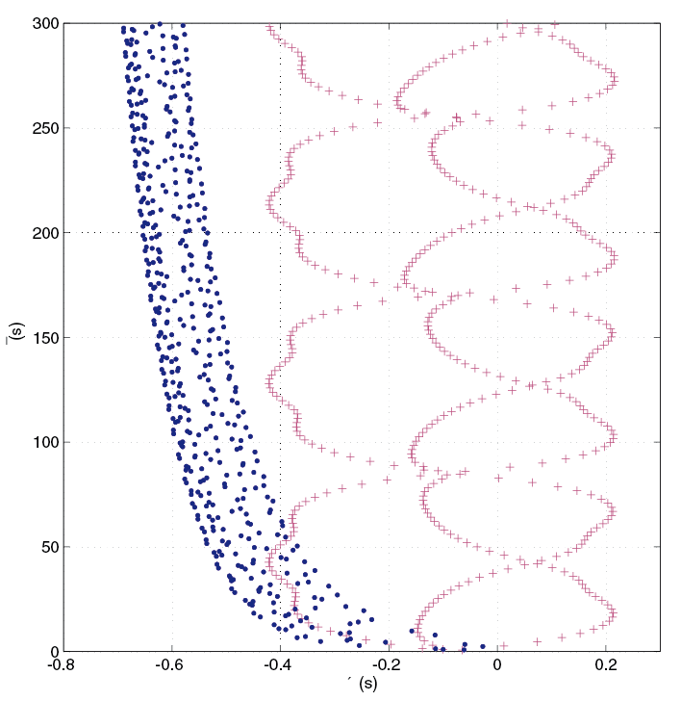QPmR algoritmus patří k nejvyužívanějším nástrojům pro analýzu spekter systémů se zpožděním. Náš tým algoritmus používá například při návrhu tvarovačů signálu [3, 4] a dalších algoritmů pro potlačení vibrací mechanických systémů [5].

Více o aktivitách výzkumného týmu lze nalézt na stránce laboratoře aplikované kybernetiky. Aplikovaný výzkum v dané oblasti probíhá též v rámci skupiny Návrh a řízení strojů a výrobků, Českého institutu informatiky, robotiky a kybernetiky, kterou vede prof. T. Vyhlídal.  

Reference

[1] Vyhlídal, T. – Zítek, P.: Mapping Based Algorithm for Large-Scale Computation of Quasi-Polynomial Zeros. IEEE Transactions on Automatic Control. 2009, vol. 54, no. 1, p. 171–177. ISSN 0018–9286. DOI: 10.1109/TAC.2008.2008345

[2] Vyhlídal, T. – Zítek, P.: QPmR – Quasi-Polynomial Root-Finder: Algorithm Update and Examples. In: Delay Systems: From Theory to Numerics and Applications. Editors: Vyhlídal T., Sipahi R., J. F. Lafay, New York: Springer, 2014, p. 299–312. ISSN 2197–117X. ISBN 978–3–319–01694–8

[3] Vyhlídal T., Hromčík M., Kučera V., Anderle M., On feedback architectures with zero vibration signal shapers, Accepted in IEEE Transaction on Automatic Control as regular paper, 15 p., DOI:10.1109/TAC.2015.2492502

[4] Vyhlídal T., Hromčík M., Parametrization of input shapers with delays of various distribution, In: AUTOMATICA, 59, 2015, pp: 256–263, DOI:10.1016/j.automatica.2015.06.025

[5] Vyhlídal, T. – Olgac, N. – Kučera, V.: Delayed resonator with acceleration feedback – Complete stability analysis by spectral methods and vibration absorber design. In: Journal of Sound and Vibration. 2014, vol. 333, no. 25, p. 6781–6795. ISSN 0022–460X. DOI:10.1016/j.jsv.2014.08.002